
慣性モーメントの導出 円錐
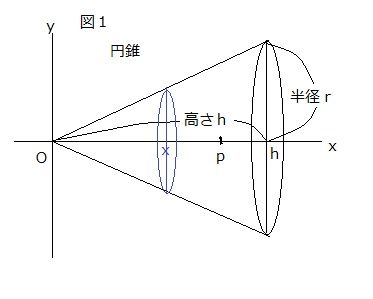
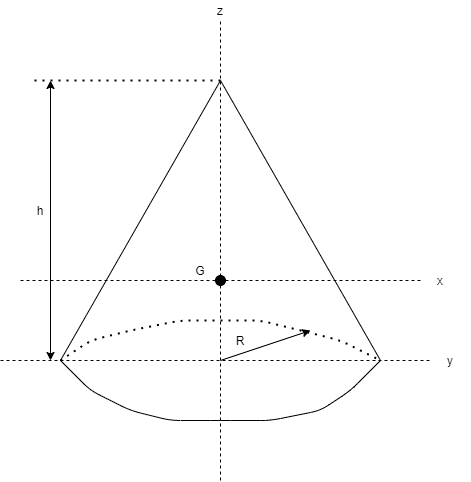
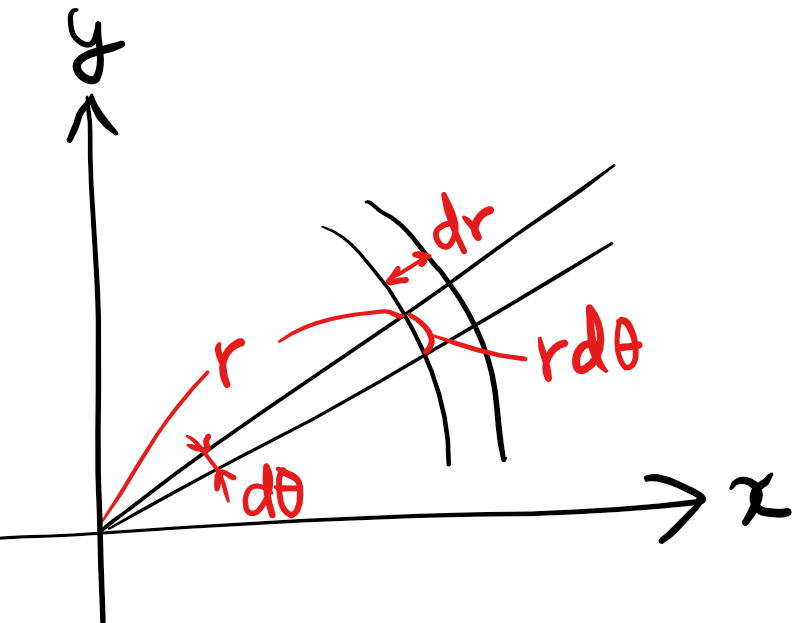
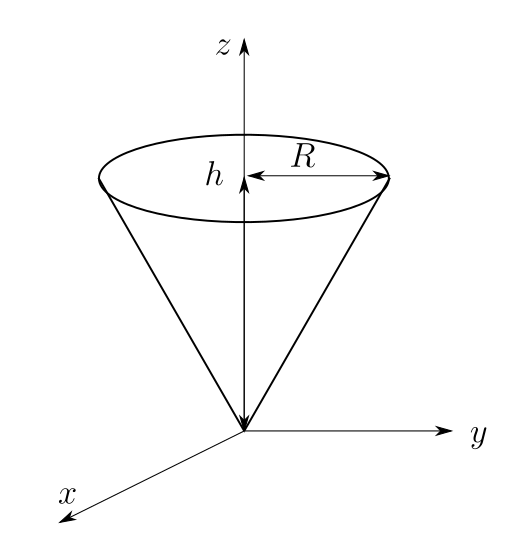
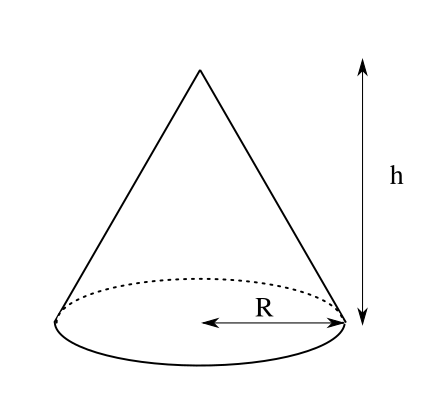
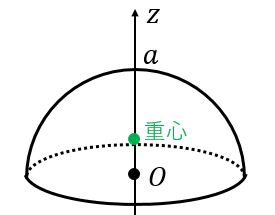
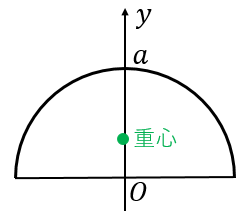
剛体の重心(2 a) このL字型の 板の重心 2 つ の 四 角 形 の 和 質量比 2:1 重心 重心 2 1 3つの正方形の和と考えてもよい 工学院大学の学生のみ利用可:印刷不可:再配布不可 (c)加藤潔18 9は剛体の密度, という記号は微小体積要素の意味で,剛体の体積 全体に渡って積分をするという意味です. 一つだけ例題を解いてみます.底面の半径 ,高さ の円錐の重心の位置を求めてみましょう.簡単のために円錐の頂点は底面の中心の垂線(図の 軸)上にあるとしましょう. 重心が 軸上にあることは対称性から明らかなので, 軸方向の重心位置だけを式(7)(8)を使って求めることにします.質量
円錐 重心 積分
円錐 重心 積分- 三角形の重心を積分で求めるのは出来ますか。 円錐の重心を求める計算と並べて比べてみるといいかもしれませんね。 同じ考え方でできる少し簡単な例でやってみると間違いが見つかりやすいと思います。 3 円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、 半径×半径×円周率×円錐の高さ×1/3 になるんだ。 これなら3秒で円錐の体積を計算でき
投稿155
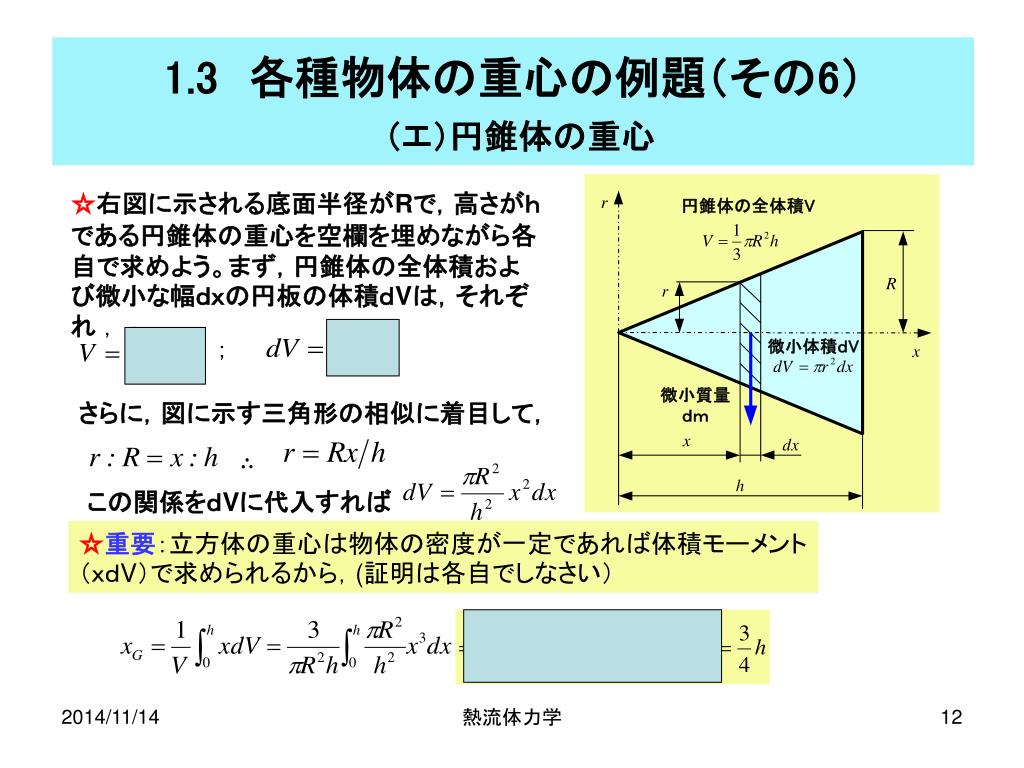
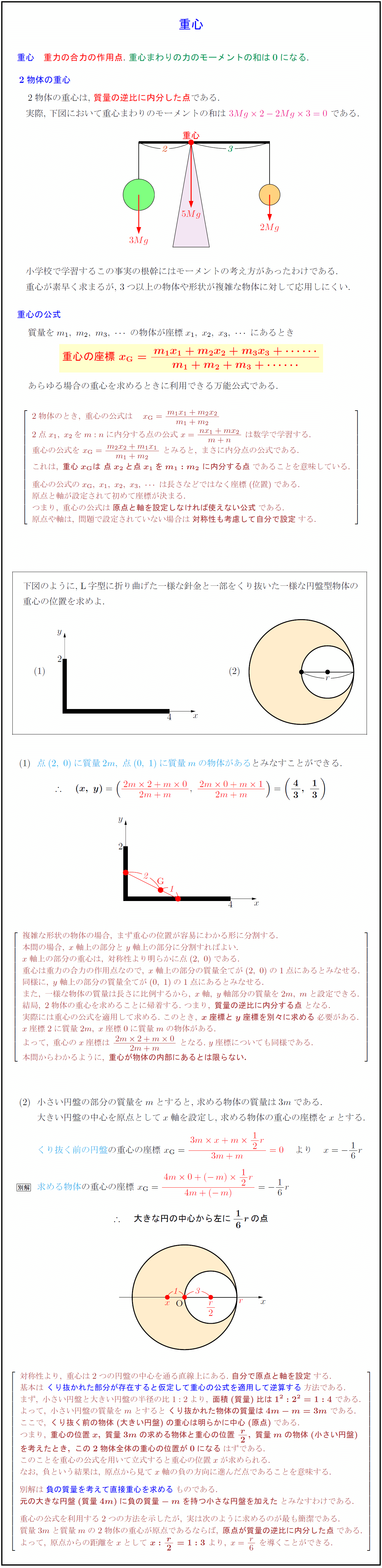
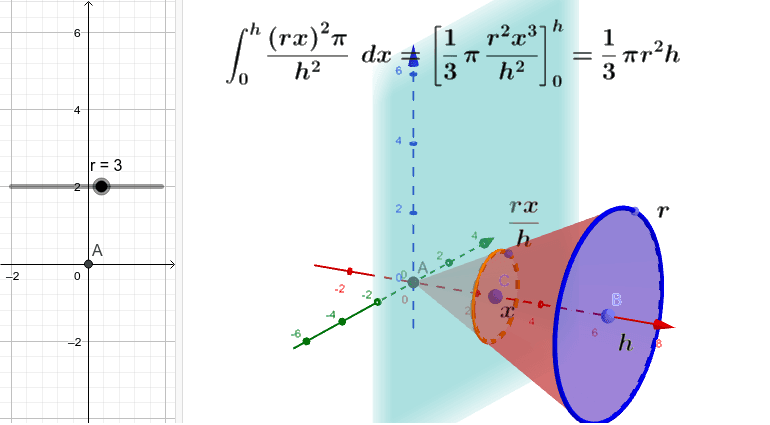
問題の解答:くり抜いた円盤の重心を求める 例題 半径2Rの円盤から、図のように半径 R 2 の円盤をくりぬいた。 この時、 残った円盤の重心の位置を答えよ。 ※いつも通り、まずは自分で考えてみましょう! 自分で解くことで、『解くうえで何が足り切り抜かれた円盤の重心 下図に示すように, 密度が一様で半径 r の円盤1から, それに内接する半径 r 2 の円盤2を切り抜いた物体について, 次の問に答えよ この物体の重心を求めよ この物体の重心を求めよ N 個の質点の位置 (または物体の重心)と質量が 積分を用いて円錐の体積 を求める以下の公式を導出します. ここで, は底面の半径, は円錐の高さとします. 証明:まず,xy平面上に原点を通る直線を考えます.この直線とx軸とのなす角をθとすると,この直線は と表せます.この直線の式とx軸および2直線 および で囲まれた図形
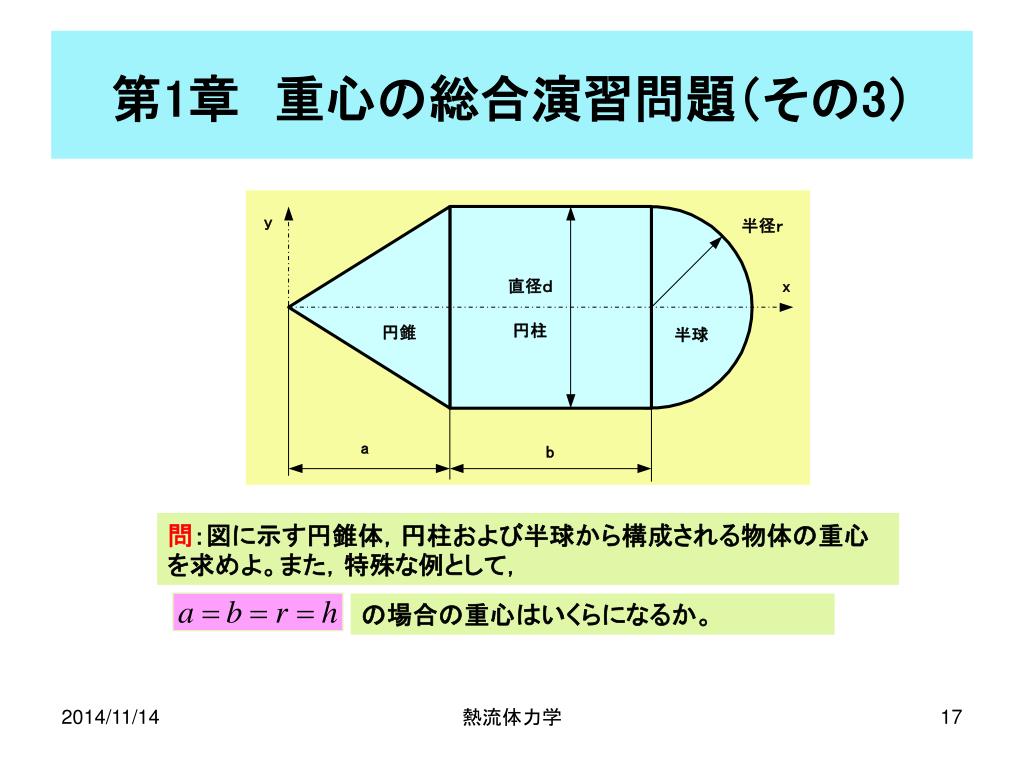
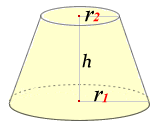
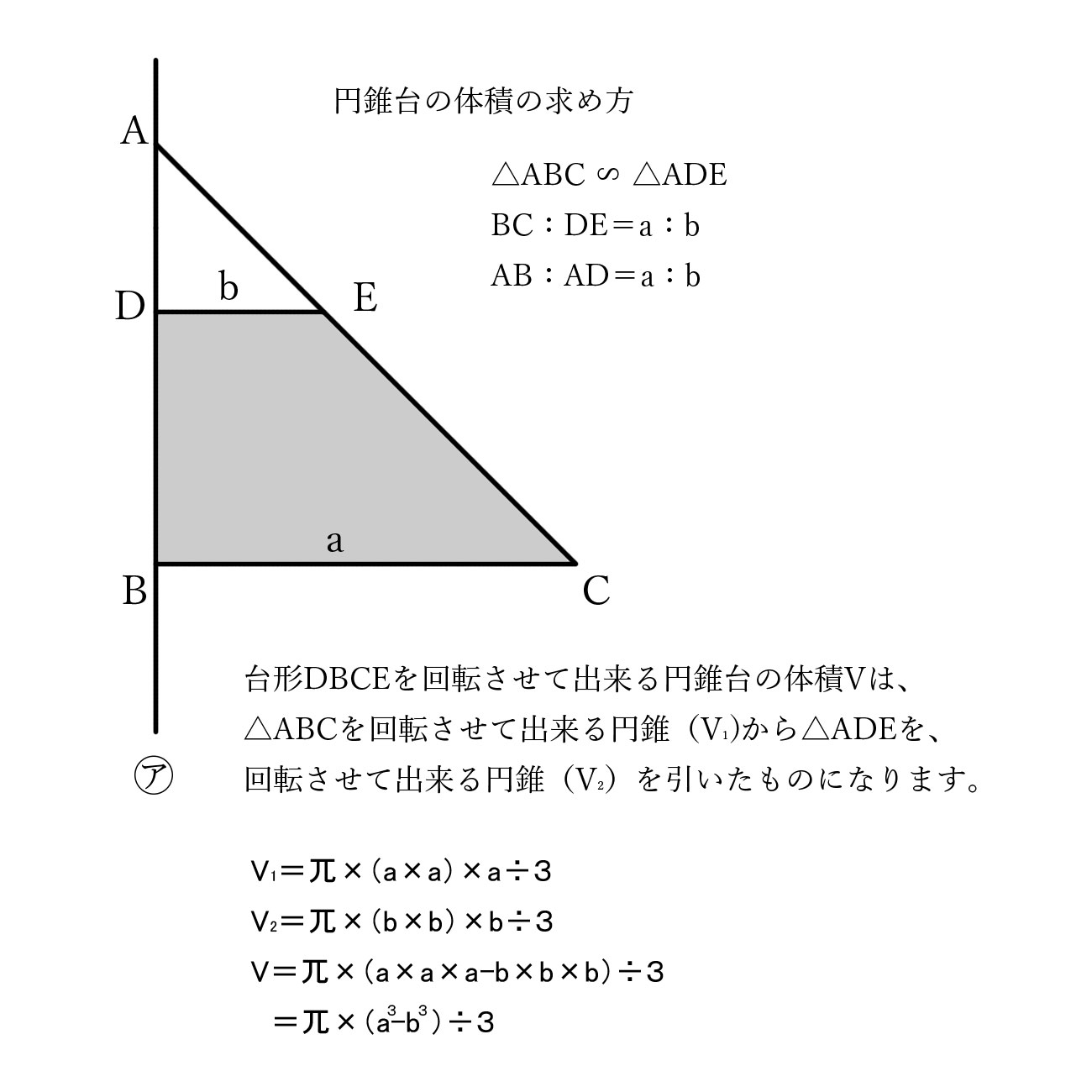
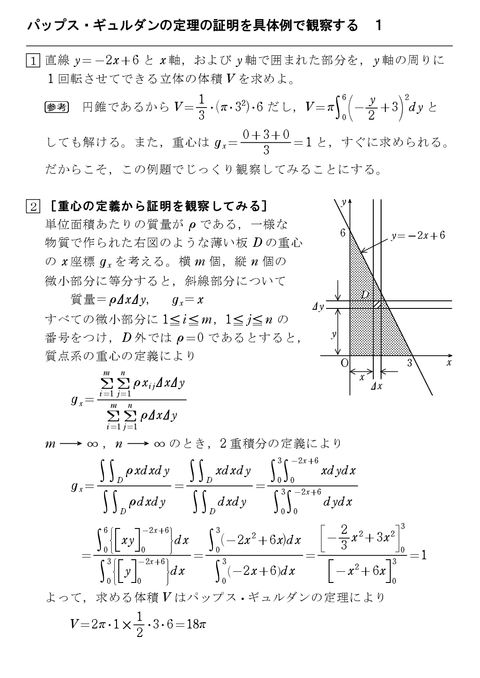
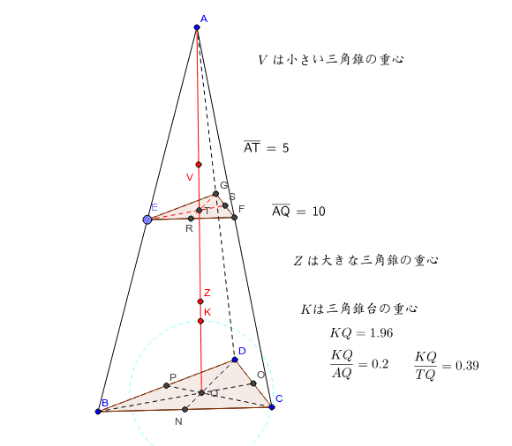
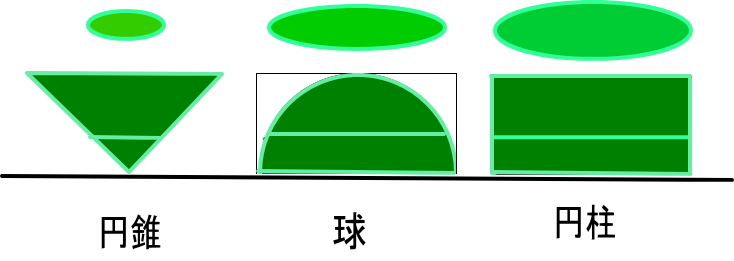
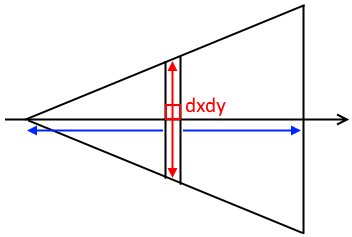
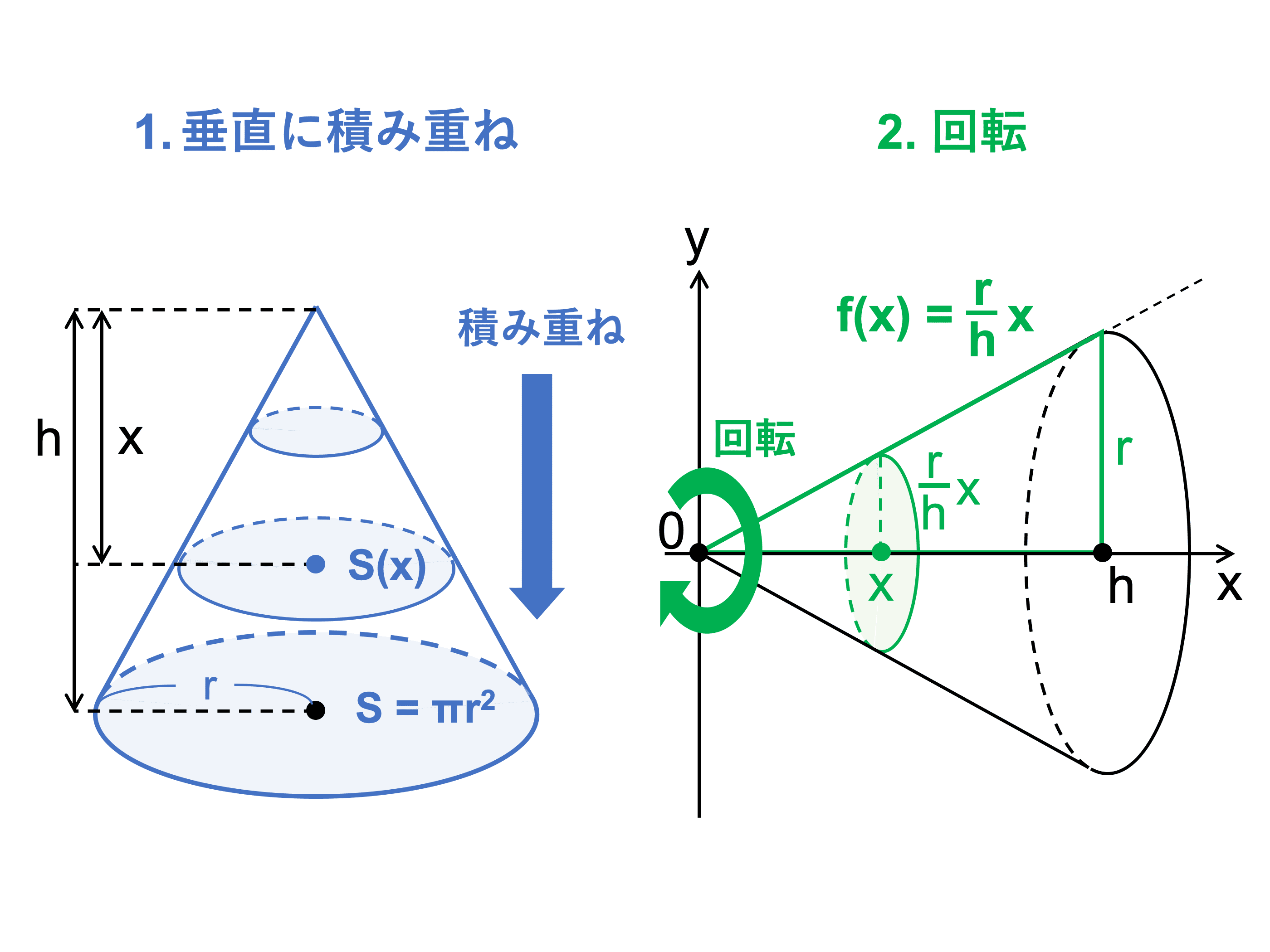
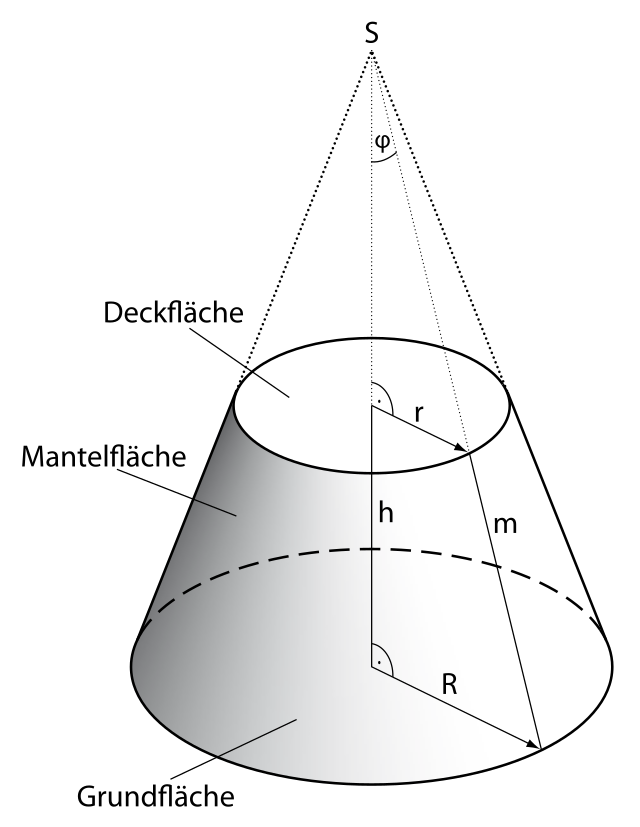
定積分の応用 §3 積分法 7定積分 (回転体の体積) 小学校や中学校で, 三角すいの体積 三角すいの体積: 球の体積: であることは,学習したと思います。 その時,「どうして円すいの体積が,円柱の体積の3分の1になっているのか? 従って、円錐全体の重心 (gx, gy, gz)はgx=gy=0であり、そして gz = Σ {n=1~h/Δz} (n (1/2)) w (n)Δz / Σ {n=1~h/Δz}w (n)Δz である。 次に、Δz→0の極限を取ると、右辺のふたつのΣ {n=1~h/Δz}Δzは定積分∫ z=0~hdzで置き換えられます。 あとはできるでしょう。 でもこれが大学数学? うーむ 0 件 通報する円錐台(えんすいだい、英 circular truncated cone )は、底面が円である錐台である。 つまり、円錐を底面に平行な平面で切り、小円錐の部分を除いた立体図形である。 プリンの形は一般的には円錐台である。受験数学、特に日本の中学入試でよく出題される立体である。
円錐 重心 積分のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「円錐 重心 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
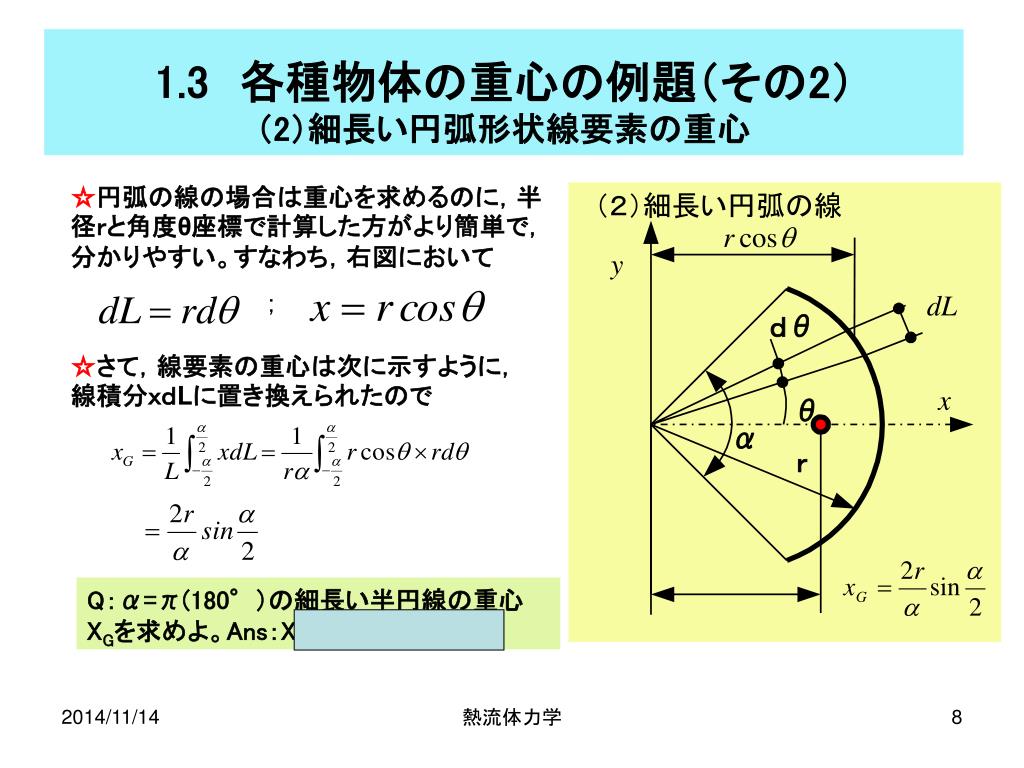
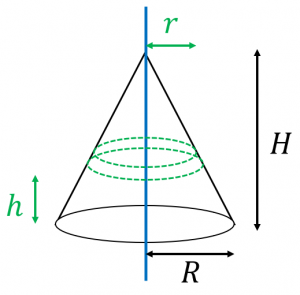
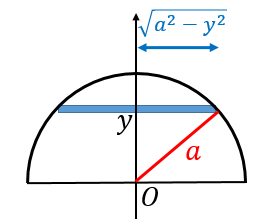
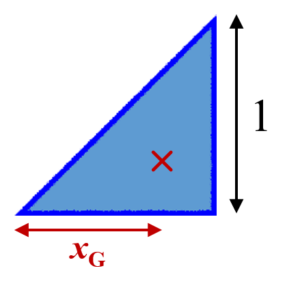
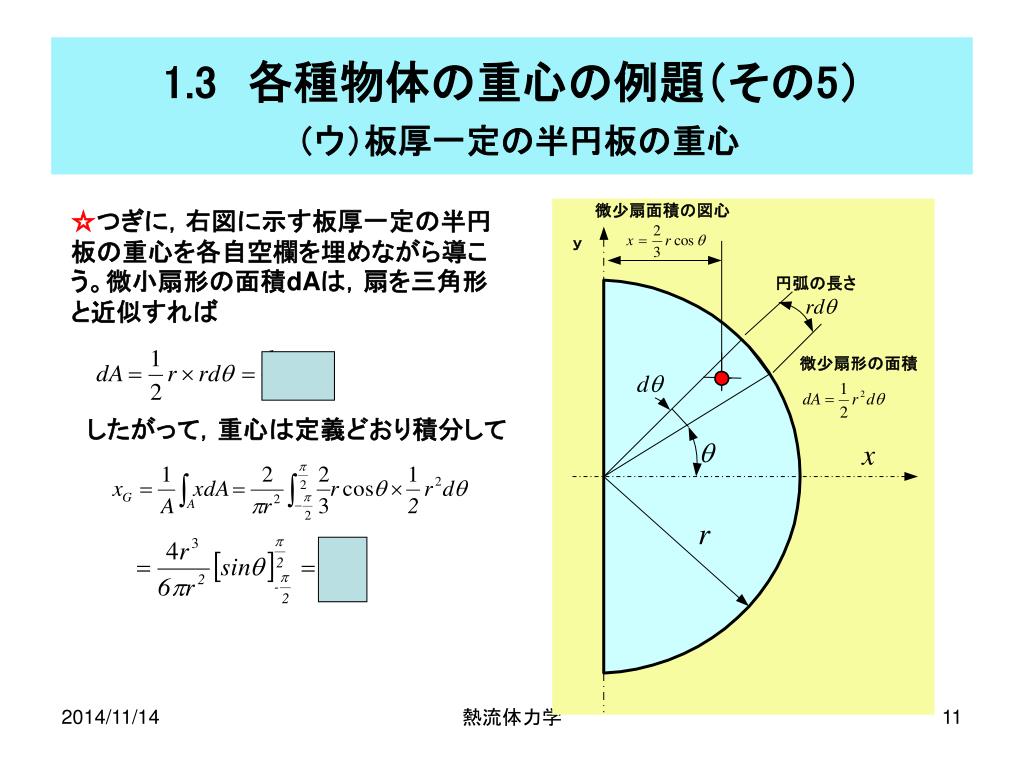
今回は積分を使って三角形の重心を求めていきたいと思います。 図形の重心は で表されます。 (「 力学半円板の重心と慣性モーメントを求めてみた 」でも使いました。 ) これを使うことで どのような図形の重心も柔軟に求めることができます 円錐の体積の計算 では円錐の体積を計算します。円柱の場合と違うのは変数\(r\)の積分が\(z\)に束縛されている点です。 そこで\(r\)を\(z\)の関数に変換する必要があります。 母線が\(z\)の関数 \ r = \cfrac{R}{h}z \ です。この関係式を使って変数変換とすると
Incoming Term: 円錐 重心 積分,




0 件のコメント:
コメントを投稿